How to Expand
Question
Expand 3(x + 2)
"Expand" means you must multiply out the brackets. You need to times everything inside the brackets (i.e. x + 2) by what's outside the brackets (3).
3(x + 2) = 3x + 6
Try these:
Expand
a) 2(x - 1)
b) 5(2 - x)
c) x(x + 3)
Did you get...?
a) 2(x - 1) = 2x - 2
b) 5(2 - x) = 10 - 5x
c) x(x + 3) = x^2 + 3x
Expand and Simplify
"Simplify" means you must write your answer as simply as possible.
For example, if you have an expression such as
3x + 2 + x + 1
you can add together the like-terms (add together the "x terms" and the number terms)
3x + 2 + x + 1 = (3x + x) + (2 + 1) = 4x + 3
In your exam, you will probably get a question like this:
Question
Expand and Simplify 2(x + 1) + 3(x - 2)
You must first expand out the brackets, and then simplify (add the like-terms):
Solution
2(x + 1) + 3(x - 2)
= 2x + 2 + 3x - 6
= 2x + 3x + 2 - 6
= 5x - 4
Try these:
Expand and simplify
a) 2(x - 1) + 5(2 - x)
b) 7(x + 3) + 2(x + 2)
Did you get...?
a) 2(x - 1) + 5(2 - x)
= 2x - 2 + 10 - 5x
= 2x - 5x - 2+ 10
= - 3x + 8
*Remember* -2 + 10 = 10 - 2 = 8
b) 7(x + 3) + 2(x + 2)
= 7x + 21 + 2x + 4
= 7x + 2x + 21 + 4
= 9x + 25
Remember:
Don't forget to multiply everything inside the brackets by the outside value. One of the most common mistakes is as follows:
3(x + 2) = 3x + 2
This is NOT CORRECT, as we have not multiplied the 2 by the 3.
3(x + 2) = 3x + 6 is correct.
Top Tip
Be careful with questions such as
Expand and Simplify 3(x + 1) - 2(x + 1)
where the two expressions in the brackets have a minus sign (-) between them. In this case, expand the brackets, but keep the second expression separate, like this:
3(x + 1) - 2(x + 1)
= 3x + 3 - [2x + 2]
Then you must take away the right-hand expression from the left:
= 3x + 3 - [2x + 2]
= 3x - 2x + 3 - 2
= x + 1
Thursday, 20 May 2010
Highest Common Factor, Least Common Multiple
Highest Common Factor (HCF)
Question
What is the HCF of 24 and 36?
To answer this question, first list the factors of 24 and 36. Remember, factors are the numbers that go into 24 and 36 (the numbers that will divide 24 and 36 exactly).
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Then the Highest Common Factor will be the highest (largest) factor that appears in both lists (common).
Solution
HCF = 12
Least Common Multiple (LCM)
Question
What is the LCM of 10 and 15?
To answer this question, first list the multiples of 10 and 15. Remember, multiples are the numbers that appear in the timestables of 10 and 15.
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, ...
Multiples of 15: 15, 30, 45, 60, 75, 90, ...
Then the Least Common Multiple will be the least (lowest) multiple that appears in both lists (common).
Solution
LCM = 30
Remember: Learn the definitions of factors and multiples so that you don't confuse yourself!
Exam Questions
Have a go at these questions:
1. What is the LCM of 24 and 36?
2. What is the HCF of 15 and 45?
3. I am thinking of two numbers.
Their LCM is 45, and their HCF is 3.
What could the two numbers be?
Hint: List the factors of 45 and the multiples of 3 to help you find possible solutions.
Send your answers to mathshints@gmail.com
(Solutions will be posted soon!)
Question
What is the HCF of 24 and 36?
To answer this question, first list the factors of 24 and 36. Remember, factors are the numbers that go into 24 and 36 (the numbers that will divide 24 and 36 exactly).
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Then the Highest Common Factor will be the highest (largest) factor that appears in both lists (common).
Solution
HCF = 12
Least Common Multiple (LCM)
Question
What is the LCM of 10 and 15?
To answer this question, first list the multiples of 10 and 15. Remember, multiples are the numbers that appear in the timestables of 10 and 15.
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, ...
Multiples of 15: 15, 30, 45, 60, 75, 90, ...
Then the Least Common Multiple will be the least (lowest) multiple that appears in both lists (common).
Solution
LCM = 30
Remember: Learn the definitions of factors and multiples so that you don't confuse yourself!
Exam Questions
Have a go at these questions:
1. What is the LCM of 24 and 36?
2. What is the HCF of 15 and 45?
3. I am thinking of two numbers.
Their LCM is 45, and their HCF is 3.
What could the two numbers be?
Hint: List the factors of 45 and the multiples of 3 to help you find possible solutions.
Send your answers to mathshints@gmail.com
(Solutions will be posted soon!)
Tuesday, 11 May 2010
Trial and Improvement
Trial and Improvement questions will always follow the same pattern - only the values will change.
Question
The solution to x^3 - x = 94 has a solution between 4 and 5.
Using Trial and Improvement, find the value of x.
Give your answer correct to one decimal place.
As the question says, the solution (the value of x we need) of the equation x^3 - x = 94 is between 4 and 5. Trial and Improvement means you must try different values of x until you find one that works for the equation. Don't forget, this question will be on your calculator paper, so remember to use it!
Start by checking the values x=4 and x=5:
x = 4
x^3 - x = 4^3 - 4 = 60
We want x^3 - x = 94, so '60' is too small.
x = 5
x^3 - x = 5^3 - 5 = 120 (too big)
So what value should we try next? x = 4.5 would be good, as it is half-way between 4 and 5.
x = 4.5
x^3 - x = 4.5^3 - 4.5 = 86.625 (too big)
In the exam, write the values you have tried in a table, like this:
x x^3 - x
4 60 Too small
5 120 Too big
4.5 86.625 Too small
If you continue to try values in this way, you will find that the solution lies between x = 4.6 and x = 4.7.
It is important to remember that you must "Give your answer correct to one decimal place", as the question states. This means the solution will be either 4.6 or 4.7 (because any number between 4.6 and 4.7 will round to either 4.6 or 4.7, accurate to one decimal place).
It makes sense to check x = 4.65 (half-way between 4.6 and 4.7)
x = 4.65
x^3 - x = 4.65^3 - 4.65 = 95.894625 (too big)
This means the solution to the equation is between 4.6 and 4.65.
Any value between 4.6 and 4.65 will, when rounded to 1 decimal place, equal 4.6.
E.g. 4.62 = 4.6 (1 decimal place), 4.649999999999 = 4.6 (1 decimal place)
Therefore, our solution, accurate to one decimal place, is x = 4.6 (because the solution is closer to 4.6 than 4.7).
Remember: You will normally have to give your answer accurate to one decimal place, or 3 significant figures, etc. Make sure you do this at the end!
Top Tip: Don't forget to show all the values you have tried. Even if you do not get the final answer correct, you can still get most of the marks if you have shown all the values of x you have checked.
MH
Question
The solution to x^3 - x = 94 has a solution between 4 and 5.
Using Trial and Improvement, find the value of x.
Give your answer correct to one decimal place.
As the question says, the solution (the value of x we need) of the equation x^3 - x = 94 is between 4 and 5. Trial and Improvement means you must try different values of x until you find one that works for the equation. Don't forget, this question will be on your calculator paper, so remember to use it!
Start by checking the values x=4 and x=5:
x = 4
x^3 - x = 4^3 - 4 = 60
We want x^3 - x = 94, so '60' is too small.
x = 5
x^3 - x = 5^3 - 5 = 120 (too big)
So what value should we try next? x = 4.5 would be good, as it is half-way between 4 and 5.
x = 4.5
x^3 - x = 4.5^3 - 4.5 = 86.625 (too big)
In the exam, write the values you have tried in a table, like this:
x x^3 - x
4 60 Too small
5 120 Too big
4.5 86.625 Too small
If you continue to try values in this way, you will find that the solution lies between x = 4.6 and x = 4.7.
It is important to remember that you must "Give your answer correct to one decimal place", as the question states. This means the solution will be either 4.6 or 4.7 (because any number between 4.6 and 4.7 will round to either 4.6 or 4.7, accurate to one decimal place).
It makes sense to check x = 4.65 (half-way between 4.6 and 4.7)
x = 4.65
x^3 - x = 4.65^3 - 4.65 = 95.894625 (too big)
This means the solution to the equation is between 4.6 and 4.65.
Any value between 4.6 and 4.65 will, when rounded to 1 decimal place, equal 4.6.
E.g. 4.62 = 4.6 (1 decimal place), 4.649999999999 = 4.6 (1 decimal place)
Therefore, our solution, accurate to one decimal place, is x = 4.6 (because the solution is closer to 4.6 than 4.7).
Remember: You will normally have to give your answer accurate to one decimal place, or 3 significant figures, etc. Make sure you do this at the end!
Top Tip: Don't forget to show all the values you have tried. Even if you do not get the final answer correct, you can still get most of the marks if you have shown all the values of x you have checked.
MH
Wednesday, 5 May 2010
Circles
These are the parts of a circle.
circumference - the perimeter (outside length) of a circle
diameter - a straight line going through the centre of a circle from one side to another
radius - a straight line from the centre to the circumference (half the diameter)
sector - the space inside two radii ("radii" is the plural of radius)
chord - a straight line from one side of a circle to another
segment - the space between a chord and the circumference
tangent - a straight line that touches the circumference at only one point
Circumference and Area
There are two formulae involving π that you should know for your exam:
Circumference = 2πr
(2 x π x r), r = radius
Area = πr^2
(π x r x r)
Note: π is a specific number used in calculating lengths and areas in circles. You do not need to remember the exact number (π = 3.14159...), but you do need to remember where the π button is on your calculator, and how to use it.
Question
Find the circumference and area of this circle
Radius, r = 4
Circumference = 2πr
= 2 x π x 4 = 8 x π
= 25.1 cm (3 significant figures)
Area = πr^2
= π x 4 x 4 = 16 x π
= 50.3 cm^2 (3s.f.)
What's Next?
Circle Theorems involving working out angles.
MH
circumference - the perimeter (outside length) of a circle
diameter - a straight line going through the centre of a circle from one side to another
radius - a straight line from the centre to the circumference (half the diameter)
sector - the space inside two radii ("radii" is the plural of radius)
chord - a straight line from one side of a circle to another
segment - the space between a chord and the circumference
tangent - a straight line that touches the circumference at only one point
Circumference and Area
There are two formulae involving π that you should know for your exam:
Circumference = 2πr
(2 x π x r), r = radius
Area = πr^2
(π x r x r)
Note: π is a specific number used in calculating lengths and areas in circles. You do not need to remember the exact number (π = 3.14159...), but you do need to remember where the π button is on your calculator, and how to use it.
Question
Find the circumference and area of this circle
Radius, r = 4
Circumference = 2πr
= 2 x π x 4 = 8 x π
= 25.1 cm (3 significant figures)
Area = πr^2
= π x 4 x 4 = 16 x π
= 50.3 cm^2 (3s.f.)
What's Next?
Circle Theorems involving working out angles.
MH
Tuesday, 4 May 2010
Keane Maths (Revision Break)
Have you ever seen Chris Moyles' Quiz Night on Channel 4? There's always a maths question, sung by famous artists.
Click here to see Keane's Maths Question. Can you get the right answer? Email your answers to mathshints@gmail.com, or comment on this post.
MH
Click here to see Keane's Maths Question. Can you get the right answer? Email your answers to mathshints@gmail.com, or comment on this post.
MH
Angles Rules
Someone has emailed asking for help with Angle Rules.
There are many questions that involve working out angles that could come up on your exam. They will usually involve two things:
- Having to work out the size of an angle
- Having to give a reason for your answer
Giving a reason for your answer simply means justifying how you worked out the size of the angle. The text in italics throughout this post are examples of the reasons you should give for the corresponding questions.
Angles on a straight line add up to 180∘
Therefore, the angle marked a will be
180 - 45 = 135∘ (angles on a straight line add up to 180∘)
Where two straight lines cross, angles such as x and 40∘in the picture are called vertically opposite angles, and are equal.
x = 40∘(vertically opposite angles)
Angles - Parallel Lines
When we have two parallel lines (marked by arrows in the picture and on your exam), and another line that crosses both parallel lines, we have a few rules about the angles that are formed.
Angle p and the angle of 40∘are called corresponding angles, and are equal.
p = 40∘(corresponding angles)
Angle q and the angle of 40∘are called alternate angles, and are equal.
q = 40∘(alternate angles)
Angle r and the angle of 40∘are called interior angles (they are both next to each other, inside the 'c' shape formed by the lines), and together they add up to 180∘.
r = 180 - 40 = 140∘(interior angles)
Remember: The properties for corresponding, alternate, and interior angles are only true if you have parallel lines.
Top Tip: Use practice papers to see what types of questions come up on this topic.
Sometimes you may be given a diagram with angles and lines, and a statement like "Brian thinks these two lines are parallel. Show that he is wrong."
When faced with this type of question, check these properties to see if they hold true, and therefore to show whether or not the lines are parallel.
What's Next?
There is lots more angle work you could revise, such as circle theorems, angles in regular polygons (regular shapes like pentagons, hexagons, etc.) Look out for posts on these in the future!
As always, send your maths questions to mathshints@gmail.com, and follow updates on Twitter.
MH
There are many questions that involve working out angles that could come up on your exam. They will usually involve two things:
- Having to work out the size of an angle
- Having to give a reason for your answer
Giving a reason for your answer simply means justifying how you worked out the size of the angle. The text in italics throughout this post are examples of the reasons you should give for the corresponding questions.
Angles on a straight line add up to 180∘
Therefore, the angle marked a will be
180 - 45 = 135∘ (angles on a straight line add up to 180∘)
Where two straight lines cross, angles such as x and 40∘in the picture are called vertically opposite angles, and are equal.
x = 40∘(vertically opposite angles)
Angles - Parallel Lines
When we have two parallel lines (marked by arrows in the picture and on your exam), and another line that crosses both parallel lines, we have a few rules about the angles that are formed.
Angle p and the angle of 40∘are called corresponding angles, and are equal.
p = 40∘(corresponding angles)
Angle q and the angle of 40∘are called alternate angles, and are equal.
q = 40∘(alternate angles)
Angle r and the angle of 40∘are called interior angles (they are both next to each other, inside the 'c' shape formed by the lines), and together they add up to 180∘.
r = 180 - 40 = 140∘(interior angles)
Remember: The properties for corresponding, alternate, and interior angles are only true if you have parallel lines.
Top Tip: Use practice papers to see what types of questions come up on this topic.
Sometimes you may be given a diagram with angles and lines, and a statement like "Brian thinks these two lines are parallel. Show that he is wrong."
When faced with this type of question, check these properties to see if they hold true, and therefore to show whether or not the lines are parallel.
What's Next?
There is lots more angle work you could revise, such as circle theorems, angles in regular polygons (regular shapes like pentagons, hexagons, etc.) Look out for posts on these in the future!
As always, send your maths questions to mathshints@gmail.com, and follow updates on Twitter.
MH
Thursday, 29 April 2010
Sine Rule (Higher Tier)
Someone has asked for information on the Sine Rule. This is a Higher Tier topic.
Sine Rule is one of the harder topics in your GCSE, but if you learn how to use it correctly, there are easy marks to be gained. This is because you don't need to remember the formula for the Sine Rule as it is on your formula sheet (in your Edexcel exam)!
Go to the inside cover of your exam and you will see the following:
In any triangle ABC
Sine Rule: a = b = c
sinA sinB sinC
It can also be written as...
sinA = sinB = sinC
a b c
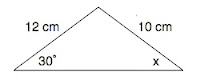
Question
In this triangle, find the size of the angle marked x.
To find the angle marked x, we can use the Sine Rule.
From the information above, we know that this relationship is true:
sin x = sin 30 (A=x, a=12, B=30, b=10 - see first triangle above)
12 10
Solution
sin x = 12sin 30 = 0.6
10
x = sin^(-1)(0.6) (inverse sine of 0.6)
x = 36.9∘ (1 decimal place)
Remember: If we have "sin x = 0.6", to get x on its own we must calculate "inverse sine of 0.6". This can be done on your calculator (normally by pressing "shift, sine" to get inverse sine).
Top Tip: When answering Sine Rule questions, write down the Sine Rule first, then substitute (put in) the values from your triangle. If you do this, you will have shown some working which will hopefully get you some marks even if your final answer is wrong.
What's Next?
Similar questions will involve having to use the Cosine Rule, or to work out the area of a triangle using sine. Both of these formulae are also on the formula sheet page of your exam. Watch out for revision posts on these topics.
Sine Rule is one of the harder topics in your GCSE, but if you learn how to use it correctly, there are easy marks to be gained. This is because you don't need to remember the formula for the Sine Rule as it is on your formula sheet (in your Edexcel exam)!
Go to the inside cover of your exam and you will see the following:
In any triangle ABC
Sine Rule: a = b = c
sinA sinB sinC
It can also be written as...
sinA = sinB = sinC
a b c
Question
In this triangle, find the size of the angle marked x.
To find the angle marked x, we can use the Sine Rule.
From the information above, we know that this relationship is true:
sin x = sin 30 (A=x, a=12, B=30, b=10 - see first triangle above)
12 10
Solution
sin x = 12sin 30 = 0.6
10
x = sin^(-1)(0.6) (inverse sine of 0.6)
x = 36.9∘ (1 decimal place)
Remember: If we have "sin x = 0.6", to get x on its own we must calculate "inverse sine of 0.6". This can be done on your calculator (normally by pressing "shift, sine" to get inverse sine).
Top Tip: When answering Sine Rule questions, write down the Sine Rule first, then substitute (put in) the values from your triangle. If you do this, you will have shown some working which will hopefully get you some marks even if your final answer is wrong.
What's Next?
Similar questions will involve having to use the Cosine Rule, or to work out the area of a triangle using sine. Both of these formulae are also on the formula sheet page of your exam. Watch out for revision posts on these topics.
Product of Prime Factors
Question
Express 240 as a product of prime factors
This question couldn't be easier! It just requires you to understand a few simple things:
- factors are the numbers that will divide a number exactly
e.g. the factors of 8 are 1, 2, 4, and 8, as these are the numbers that divide 8 exactly
the factors of 35 are 1, 5, 7, 35
- prime numbers are numbers that have only two factors: 1 and itself
e.g. 7 is a prime number, because its factors are 1 and 7
11 is a prime number, because its factors are 1 and 11
1 is not a prime number as it has only one factor
- a product is a multiplication
e.g. 2 x 3 is a product
7 x 11 x 13 is a product
Solution
We must split 240 up into a product of prime factors.
- Choose prime numbers that go into 240 to form a factor tree, as shown below.
- Start by seeing if 2 goes into 240, and keep doing this until it no longer divides the number you get.
- Then try 3, then 5, 7, 11, 13, etc. (the prime numbers).
- Stop when you get to a prime number.
240
/ \
2 120 (240 = 2 x 120)
/ \
2 60 (120 = 2 x 60)
/ \
2 30 (60 = 30 x 2)
/ \
2 15 (30 = 2 x 15)
/ \
3 5
We can express 240 as a product of the prime factors from our tree (2, 2, 2, 2, 3, 5)
Answer: 240 = 2 x 2 x 2 x 2 x 3 x 5
Remember: The solution is not complete unless you write "240 = 2 x 2 x 2 x 2 x 3 x 5", as this is the product of prime factors. You will lose marks if you do not finish the question in this way.
Top Tip: Practise this question with lots of different numbers (you choose!), and you're bound to get it right in the exam.
Don't forget you can email your maths questions to mathshints@gmail.com, and follow us on Twitter!
Express 240 as a product of prime factors
This question couldn't be easier! It just requires you to understand a few simple things:
- factors are the numbers that will divide a number exactly
e.g. the factors of 8 are 1, 2, 4, and 8, as these are the numbers that divide 8 exactly
the factors of 35 are 1, 5, 7, 35
- prime numbers are numbers that have only two factors: 1 and itself
e.g. 7 is a prime number, because its factors are 1 and 7
11 is a prime number, because its factors are 1 and 11
1 is not a prime number as it has only one factor
- a product is a multiplication
e.g. 2 x 3 is a product
7 x 11 x 13 is a product
Solution
We must split 240 up into a product of prime factors.
- Choose prime numbers that go into 240 to form a factor tree, as shown below.
- Start by seeing if 2 goes into 240, and keep doing this until it no longer divides the number you get.
- Then try 3, then 5, 7, 11, 13, etc. (the prime numbers).
- Stop when you get to a prime number.
240
/ \
2 120 (240 = 2 x 120)
/ \
2 60 (120 = 2 x 60)
/ \
2 30 (60 = 30 x 2)
/ \
2 15 (30 = 2 x 15)
/ \
3 5
We can express 240 as a product of the prime factors from our tree (2, 2, 2, 2, 3, 5)
Answer: 240 = 2 x 2 x 2 x 2 x 3 x 5
Remember: The solution is not complete unless you write "240 = 2 x 2 x 2 x 2 x 3 x 5", as this is the product of prime factors. You will lose marks if you do not finish the question in this way.
Top Tip: Practise this question with lots of different numbers (you choose!), and you're bound to get it right in the exam.
Don't forget you can email your maths questions to mathshints@gmail.com, and follow us on Twitter!
Estimate
Someone has asked for a post on the following type of question.
Question
Estimate the value of
272 x 47.7
0.531
In this question, you must simply do the following:
- round all the numbers to 1 significant figure
- do the calculation
Solution
272 = 300 (1 significant figure)
47.7 = 50 (1s.f.)
0.531 = 0.5 (1s.f.)
So the calculation you must do is
300 x 50 = 15000 = 15000 x 2 = 30000
0.5 0.5
Remember: dividing by 0.5 is the same as multiplying by 2
Top Tip: Don't rush into getting an answer. Read and understand what the question asks you to do. Here you need an estimate, not an exact answer.
MH
Question
Estimate the value of
272 x 47.7
0.531
In this question, you must simply do the following:
- round all the numbers to 1 significant figure
- do the calculation
Solution
272 = 300 (1 significant figure)
47.7 = 50 (1s.f.)
0.531 = 0.5 (1s.f.)
So the calculation you must do is
300 x 50 = 15000 = 15000 x 2 = 30000
0.5 0.5
Remember: dividing by 0.5 is the same as multiplying by 2
Top Tip: Don't rush into getting an answer. Read and understand what the question asks you to do. Here you need an estimate, not an exact answer.
MH
Monday, 26 April 2010
Mode, Median, Mean & Range - (Stem and Leaf)
Sometimes in your exam the question will already have a completed Stem and Leaf diagram, and you will be asked questions about it.
Question
Below is a Stem and Leaf Diagram of the ages of music shop customers
Key: 1 | 7 = 17
a) What is the modal age of customer?
"Modal" means work out the mode from your data.
Mode = most common value
Solution: mode = 17 (17 is the value that appears the most often in the Sem and Leaf diagram)
b) What is the median age of customer?
Median = middle value
There are 12 values in the table, so the middle value will be half-way between the 6th and 7th values.
Cross off the data in the Stem and Leaf diagram until you get to the middle values (crossing off from each end as you go along):
You cannot have two medians, so the median will be half-way between 1 and 3.
Solution: median = 2
c) Work out the range
Range = difference between highest value and lowest value (= highest value - lowest value)
The highest value is 31. The lowest value is 17.
Solution: range = 31 - 17 = 14
d) Find the mean
Mean = total of all pieces of data ÷ number of pieces of data
To work out the mean age of customer, you must add up all the ages (to get the total of all pieces of data) and divide by the number of customers (the number of pieces of data, 12).
Solution: 17 + 17 + 17 + 18 + 21 + 21 + 23 + 23 + 24 + 26 + 28 + 31 = 266
266 ÷ 12 = 22.1666...
Mean = 22.2 (1 decimal place)
Remember:
- Learn the definitions of mode, median, mean and range
Top Tip: These questions will probably be the same if they come up in your exam, so practice them well as only the values will change.
Question
Below is a Stem and Leaf Diagram of the ages of music shop customers
Key: 1 | 7 = 17
a) What is the modal age of customer?
"Modal" means work out the mode from your data.
Mode = most common value
Solution: mode = 17 (17 is the value that appears the most often in the Sem and Leaf diagram)
b) What is the median age of customer?
Median = middle value
There are 12 values in the table, so the middle value will be half-way between the 6th and 7th values.
Cross off the data in the Stem and Leaf diagram until you get to the middle values (crossing off from each end as you go along):
You cannot have two medians, so the median will be half-way between 1 and 3.
Solution: median = 2
c) Work out the range
Range = difference between highest value and lowest value (= highest value - lowest value)
The highest value is 31. The lowest value is 17.
Solution: range = 31 - 17 = 14
d) Find the mean
Mean = total of all pieces of data ÷ number of pieces of data
To work out the mean age of customer, you must add up all the ages (to get the total of all pieces of data) and divide by the number of customers (the number of pieces of data, 12).
Solution: 17 + 17 + 17 + 18 + 21 + 21 + 23 + 23 + 24 + 26 + 28 + 31 = 266
266 ÷ 12 = 22.1666...
Mean = 22.2 (1 decimal place)
Remember:
- Learn the definitions of mode, median, mean and range
Top Tip: These questions will probably be the same if they come up in your exam, so practice them well as only the values will change.
Stem and Leaf Diagrams - Drawing
Most topics in your GCSE Maths are quite straight forward and simply require you to follow set rules. Stem and Leaf questions are an example of this type of question.
You will be given a set of data.
Question
The ages of 12 music shop customers are recorded below.
28 17 21 23 18 17 31 23 24 17 21 26
Draw an ordered Stem and Leaf Diagram for these data.
The question helps you remember that data in a Stem and Leaf diagram needs to be ordered, so start by writing out the data in order (lowest to highest):
17 17 17 18 21 21 23 23 24 26 28 31
Then you put the digit from the tens (1, 2, 3) on the left, draw a vertical line, and fill in the rest of the diagram, as shown below. 1 | 7 7 7 8
(1 | 7 7 7 8 represents 17, 17, 17, 18, and so on)
The Stem and Leaf diagram is not complete without a key. A key is simply an explanation of what the data means in your diagram. For example:
Key: 1 | 7 = 17
Remember:
- Order the data in your diagram
- Include a key
What's next?
How to work out mode, median, mean and range from your Stem and Leaf diagram.
Top Tip: It's much easier to tackle these types of questions if the rules come naturally to you. It's important to practice questions enough so that you know exactly what to do without having to look it up in your notes.
Don't hesitate to leave comments on the blog, or email mathshints@gmail.com with more questions on this or any topic.
MH
You will be given a set of data.
Question
The ages of 12 music shop customers are recorded below.
28 17 21 23 18 17 31 23 24 17 21 26
Draw an ordered Stem and Leaf Diagram for these data.
The question helps you remember that data in a Stem and Leaf diagram needs to be ordered, so start by writing out the data in order (lowest to highest):
17 17 17 18 21 21 23 23 24 26 28 31
Then you put the digit from the tens (1, 2, 3) on the left, draw a vertical line, and fill in the rest of the diagram, as shown below. 1 | 7 7 7 8
(1 | 7 7 7 8 represents 17, 17, 17, 18, and so on)
The Stem and Leaf diagram is not complete without a key. A key is simply an explanation of what the data means in your diagram. For example:
Key: 1 | 7 = 17
Remember:
- Order the data in your diagram
- Include a key
What's next?
How to work out mode, median, mean and range from your Stem and Leaf diagram.
Top Tip: It's much easier to tackle these types of questions if the rules come naturally to you. It's important to practice questions enough so that you know exactly what to do without having to look it up in your notes.
Don't hesitate to leave comments on the blog, or email mathshints@gmail.com with more questions on this or any topic.
MH
Sunday, 25 April 2010
Welcome
Welcome to Maths Hints.
Here you will find useful tips on how to revise for your exams, as well as techniques on how to answer exam questions. Revision topics will also be posted for both Higher and Foundation tier exams.
If you have a question on a specific maths topic, please send this to mathshints@gmail.com along with which tier you are studying (Higher or Foundation) and your question will be answered on this blog. Your name and email address will not be published.
Good luck with revision!
MH
Here you will find useful tips on how to revise for your exams, as well as techniques on how to answer exam questions. Revision topics will also be posted for both Higher and Foundation tier exams.
If you have a question on a specific maths topic, please send this to mathshints@gmail.com along with which tier you are studying (Higher or Foundation) and your question will be answered on this blog. Your name and email address will not be published.
Good luck with revision!
MH
Subscribe to:
Comments (Atom)