Sine Rule (Higher Tier)

Someone has asked for information on the Sine Rule. This is a Higher Tier topic.

Sine Rule is one of the harder topics in your GCSE, but if you learn how to use it correctly, there are easy marks to be gained. This is because you don't need to remember the formula for the Sine Rule as it is on your formula sheet (in your Edexcel exam)!

Go to the inside cover of your exam and you will see the following:

In any triangle ABC

Sine Rule:    a    =    b    =    c  
                 sinA     sinB      sinC




It can also be written as...

sinA  =  sinB  =  sinC
  a           b           c

Question

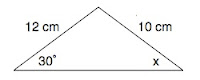
In this triangle, find the size of the angle marked x.



To find the angle marked x, we can use the Sine Rule.

From the information above, we know that this relationship is true:

sin x   =   sin 30      (A=x, a=12, B=30, b=10 - see first triangle above)
  12            10

Solution

sin x = 12sin 30  = 0.6
                10 
x = sin^(-1)(0.6)         (inverse sine of 0.6)
x = 36.9∘ (1 decimal place)

Remember: If we have "sin x = 0.6", to get x on its own we must calculate "inverse sine of 0.6". This can be done on your calculator (normally by pressing "shift, sine" to get inverse sine).

Top Tip: When answering Sine Rule questions, write down the Sine Rule first, then substitute (put in) the values from your triangle. If you do this, you will have shown some working which will hopefully get you some marks even if your final answer is wrong.

What's Next?
Similar questions will involve having to use the Cosine Rule, or to work out the area of a triangle using sine. Both of these formulae are also on the formula sheet page of your exam. Watch out for revision posts on these topics.

Product of Prime Factors

Question
Express 240 as a product of prime factors

This question couldn't be easier! It just requires you to understand a few simple things:

- factors are the numbers that will divide a number exactly
e.g. the factors of 8 are 1, 2, 4, and 8, as these are the numbers that divide 8 exactly
       the factors of 35 are 1, 5, 7, 35

- prime numbers are numbers that have only two factors: 1 and itself
e.g. 7 is a prime number, because its factors are 1 and 7
      11 is a prime number, because its factors are 1 and 11
      1 is not a prime number as it has only one factor

- a product is a multiplication
e.g. 2 x 3 is a product
       7 x 11 x 13 is a product

Solution
We must split 240 up into a product of prime factors.
- Choose prime numbers that go into 240 to form a factor tree, as shown below. 
- Start by seeing if 2 goes into 240, and keep doing this until it no longer divides the number you get. 
- Then try 3, then 5, 7, 11, 13, etc. (the prime numbers). 
- Stop when you get to a prime number.

                240
               /      \
             2      120                     (240 = 2 x 120)
                    /      \
                  2       60                 (120 = 2 x 60)
                         /      \
                       2       30            (60 = 30 x 2)
                              /      \
                            2       15       (30 = 2 x 15)
                                   /      \
                                 3        5

We can express 240 as a product of the prime factors from our tree (2, 2, 2, 2, 3, 5)

Answer: 240 = 2 x 2 x 2 x 2 x 3 x 5

Remember: The solution is not complete unless you write "240 = 2 x 2 x 2 x 2 x 3 x 5", as this is the product of prime factors. You will lose marks if you do not finish the question in this way.

Top Tip: Practise this question with lots of different numbers (you choose!), and you're bound to get it right in the exam.


Don't forget you can email your maths questions to mathshints@gmail.com, and follow us on Twitter!

Estimate

Someone has asked for a post on the following type of question.

Question
Estimate the value of 

272 x 47.7 
   0.531


In this question, you must simply do the following:
- round all the numbers to 1 significant figure
- do the calculation

Solution

272 = 300 (1 significant figure)
47.7 = 50 (1s.f.)
0.531 = 0.5 (1s.f.)

So the calculation you must do is    
300 x 50  = 15000  = 15000 x 2  = 30000
    0.5            0.5

Remember: dividing by 0.5 is the same as multiplying by 2


Top Tip: Don't rush into getting an answer. Read and understand what the question asks you to do. Here you need an estimate, not an exact answer.

MH

Mode, Median, Mean & Range - (Stem and Leaf)

Sometimes in your exam the question will already have a completed Stem and Leaf diagram, and you will be asked questions about it.

Question
Below is a Stem and Leaf Diagram of the ages of music shop customers

Key: 1 | 7 = 17







a) What is the modal age of customer?

"Modal" means work out the mode from your data.

Mode = most common value

Solution: mode = 17    (17 is the value that appears the most often in the Sem and Leaf diagram)


b) What is the median age of customer?

Median = middle value

There are 12 values in the table, so the middle value will be half-way between the 6th and 7th values.
Cross off the data in the Stem and Leaf diagram until you get to the middle values (crossing off from each end as you go along):

You cannot have two medians, so the median will be half-way between 1 and 3.

Solution: median = 2


c) Work out the range

Range = difference between highest value and lowest value    (= highest value - lowest value)

The highest value is 31. The lowest value is 17.

Solution: range = 31 - 17 = 14


d) Find the mean

Mean = total of all pieces of data ÷ number of pieces of data

To work out the mean age of customer, you must add up all the ages (to get the total of all pieces of data) and divide by the number of customers (the number of pieces of data, 12).

Solution: 17 + 17 + 17 + 18 + 21 + 21 + 23 + 23 + 24 + 26 + 28 + 31 = 266
266 ÷ 12 = 22.1666... 
Mean = 22.2 (1 decimal place)

Remember:
- Learn the definitions of mode, median, mean and range


Top Tip: These questions will probably be the same if they come up in your exam, so practice them well as only the values will change.

Stem and Leaf Diagrams - Drawing

Most topics in your GCSE Maths are quite straight forward and simply require you to follow set rules. Stem and Leaf questions are an example of this type of question.

You will be given a set of data.

Question
The ages of 12 music shop customers are recorded below.

28    17    21    23    18    17    31    23    24    17    21    26


Draw an ordered Stem and Leaf Diagram for these data.

The question helps you remember that data in a Stem and Leaf diagram needs to be ordered, so start by writing out the data in order (lowest to highest):

17    17    17    18    21    21    23    23    24    26    28   31

Then you put the digit from the tens (1, 2, 3) on the left, draw a vertical line, and fill in the rest of the diagram, as shown below.  1  |  7 7 7 8

(1  |  7 7 7 8 represents 17, 17, 17, 18, and so on)

The Stem and Leaf diagram is not complete without a key. A key is simply an explanation of what the data means in your diagram. For example:

Key:    1 | 7 = 17


Remember:
- Order the data in your diagram
- Include a key

What's next?
How to work out mode, median, mean and range from your Stem and Leaf diagram. 

Top Tip: It's much easier to tackle these types of questions if the rules come naturally to you. It's important to practice questions enough so that you know exactly what to do without having to look it up in your notes.

Don't hesitate to leave comments on the blog, or email mathshints@gmail.com with more questions on this or any topic.

MH

Welcome

Welcome to Maths Hints.

Here you will find useful tips on how to revise for your exams, as well as techniques on how to answer exam questions. Revision topics will also be posted for both Higher and Foundation tier exams.

If you have a question on a specific maths topic, please send this to mathshints@gmail.com along with which tier you are studying (Higher or Foundation) and your question will be answered on this blog. Your name and email address will not be published.

Good luck with revision!

MH